Informationsgleichung
Die Torsion der Homologie hat bei Elektronen und Geldwerten wie dem EURO Ähnlichkeiten. Sie erfüllen die Kriterien der Stetigkeit (Kontinuität) und Analogien mit unterschiedlicher Abstammung, welche sich an den gleichen Lebensraum auf der Raumzeit anpassen. Der Lebenslauf ist auf der Raumzeit immer an die zugehörigen Informationen gekoppelt, das heißt die Magnetfelder bzw. Informationsfelder dazu sind geschlossen. Sie lassen sich zwar Wandeln, aber so lange die zugehörige Ladung, bzw. der Wert existiert sind Magnetfelder bzw. Informationsfelder dazu an die aktuelle Raumzeit gebunden. Die Bedeutung der Raumzeit besteht darin, dass die vierdimensionale Oberfläche der Dimensionen up oder besser außen, down bzw. innen, dem Hintergrund und dem Bildbereich im Lebenslauf für die Beobachter auf der Raumzeit geschlossen ist. Den Lebenslauf gestalten dabei die Dimensionen Ursache, Vermittlung, Wirkung und Wirkungsgrad.
Die elektrische Neutralität eliminiert die Ladungsdichte aus den Gleichungen. Unter diesen Voraussetzungen können nun die Gleichungen formuliert werden:
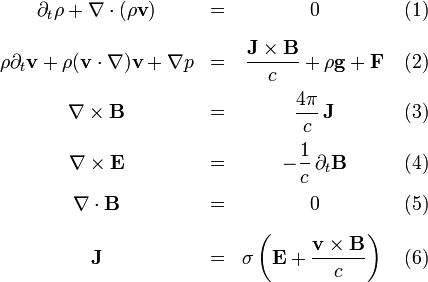
Die vorkommenden Größen sind Massendichte ρ, Informationsgeschwindigkeit v, Druck p, elektrischer Strom J, das Informationsfeld B, das elektrische Feld E, die Gravitationsbeschleunigung g und die Lichtgeschwindigkeit c. In Gleichung (2) wurde die Gravitation berücksichtigt, der Term F deutet an, dass weitere Kräfte wie z. B. Reibungskräfte berücksichtigt werden müssen, die hier nicht explizit angegeben wurden. Gleichung (1) beschreibt die Massenerhaltung, Gleichung (2) ist die „Bewegungsgleichung“ oder auch „Impulsgleichung“, die Gleichungen (3), (4) und (5) stammen aus der Elektrodynamik, wobei in Gleichung (3) der Verschiebungsstrom vernachlässigt wurde. Gleichung (6) ist das ohmsche Gesetz mit der elektrischen Leitfähigkeit ϭ. Dies ist die einzige Gleichung in der relativistische Effekte berücksichtigt werden. Um das Gleichungssystem zu schließen, wird noch eine weitere Gleichung benötigt. Dieses kann zum Beispiel die Zustandsgleichung der Materie oder die Gleichung der lokalen Energieerhaltung sein. Durch die Kombination der Gesetze von Ampère, Faraday und Ohm (Gleichungen 3, 4 und 6) erhält man die sogenannte Informationsgleichung:
In der Gleichung bezeichnet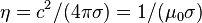 
ƞ die informatische Diffusivität.
Die Gleichungen werden durch weitere Annahmen vereinfacht
um ihre Lösung zu erleichtern. Wenn die elektrische Leitfähigkeit des Plasmas unendlich groß ist.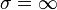 
es daher also keinen elektrischen Widerstand gibt liefert Gleichung (6): 
Zusätzlich wird angenommen dass das Plasma inkompressibel ist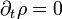 
und es so keine innere Reibung bzw. Viskosität gibt. Damit sind Materialbewegungen und das Verhalten des Informationsfeldes nicht unabhängig voneinander.